Z gréckeho významu znamená matematika „milovať poznanie“ a v jednoduchosti by sme mohli povedať že sa zaoberá štúdiom diagramov a čísel. A medzi tými všetkými číslami, ktoré poznáme vystupujú dve, ktoré sú výnimočné, najznámejšie, najužitočnejšie. Sú to dve nekonečné konštanty a to π a e. Čo o nich vlastne viete?
π (Pí) = 3,14159265359
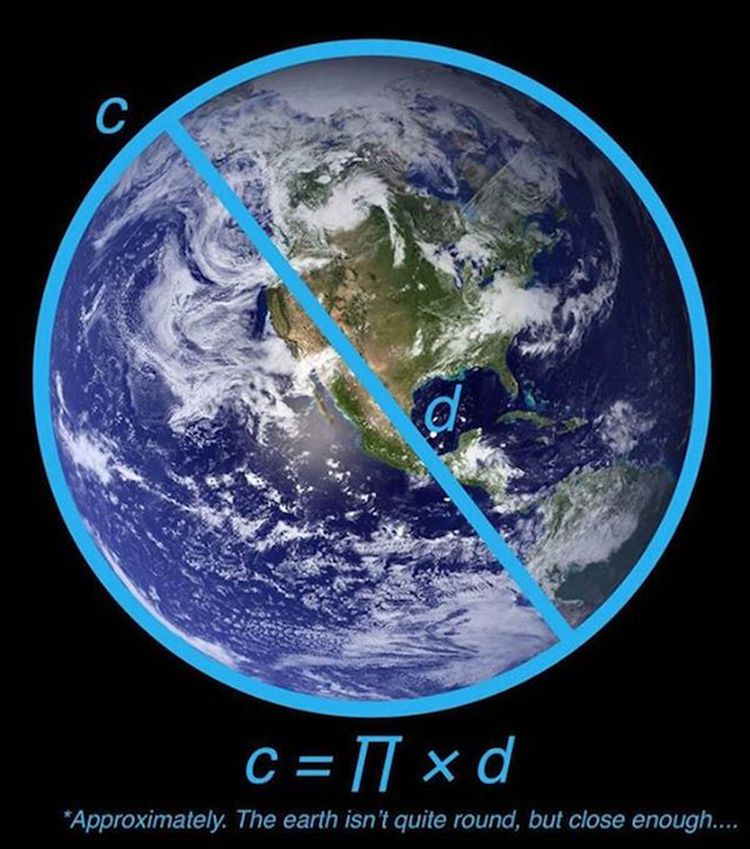
Pí je kráľom (alebo kráľovná?) medzi číslami. Ludolfovo číslo, ako sa pí oficiálne nazýva, je číslo iracionálne, teda jeho rozvoj za desatinou čiarkou pokračuje stále ďalej a ďalej až do nekonečna. Pí je výsledkom dĺžky obvodu kruhu vydeleného jeho priemerom. Z takejto definície je zjavné, že pí nezávisí od veľkosti daného kruhu. Či už je kruh maličký, alebo veľký ako naša Zem, pri takomto výpočte vám stále vyjde π.
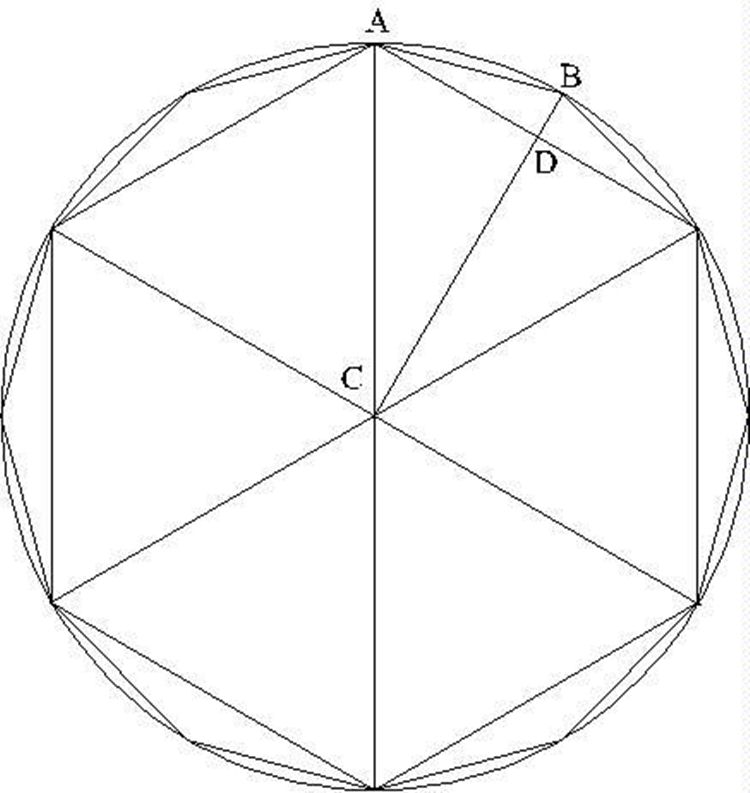
Za prvého človeka, ktorý sa o toto číslo zaujímal, sa pokladá samotný Archimedes, jeden z najväčších matematikov nielen staroveku, ale celej histórie ľudstva, ktorý v roku 255 p.n.l. predložil matematický postup výpočtu Pí. Súvis medzi obvodom a priemerom kruhu si však už oveľa skôr všimli starí Babylončania. Archimedovi sa ako prvému podarilo pomocou výpočtov obvodu vpísaného a opísaného 96-uholníka (pri výpočtoch si ich rozdelil na 3-uholníky) odhadnúť približnú hodnotu slávneho pí. Podľa jeho výpočtov sa táto konštanta nachádza v tomto intervale 3,1408 < π <3,1428.
Od tohto momentu začalo π naberať na sláve a stalo sa elitou medzi číslami. Jeho využitie v staroveku bolo hlavne pri výpočtoch miery, napríklad veľkosti pozemkov kráľov či menších zemepánov, pri rozdeľovaní pôdy medzi dedičov atď. Svoj oficiálny názov, Ludolfovo číslo, však π dostalo po holandsko-nemeckom matematikovi menom Ludolph van Ceulen, ktorý Archimedovou metodikou v roku 1596 určil π na 20 desatinných miest.

Číslom π bolo fascinovaných mnoho matematikov histórie, skúmali jeho vlastnosti a pokúšali sa určiť čo najviac číslic za jeho desatinou čiarkou. V roku 1768 dokázal Johann Lambert, že π je iracionálne, teda jeho rozvoj je nekonečný a ďalší matematici sa mohli naháňať, kto ho určí presnejšie. O viac ako 100 rokov, v roku 1882 dokázal Ferdinand von Lindemann, že π je transcendentné a teda v celom vesmíre neexistuje žiadna algebraická rovnica, ktorej riešením by bolo π. Dnes poznáme viac ako 10 000 000 000 000 číslic za desatinou čiarkou, ktoré sa v π nachádzajú. Niet pochýb, veď ide o najznámejšie číslo, ktoré pozná každý z nás, no nie?
Eulerove číslo – e = 2,7182818284…
V porovnaním s π je Eulerova konštanta len slabým odvarom, no i tak má v matematike veľmi dôležité postavenie, ktoré jej nemožno odoprieť. Možno je to kvôli tomu, že oproti π je e ešte mladým číslom a teda jeho oslnivá kariéra ho možno len čaká. Jeho najväčší význam tkvie v tom, že je používaný ako základ prirodzeného logaritmu. Eulerova konštanta sa využíva všade tam, kde sa skúma rast určitej veličiny, či už ide o počet obyvateľov, bankové úroky alebo fyzikálne veličiny.

Číslo e je od π mladšie o celých 1900 rokov. Napriek tomu, že sa nazýva Eulerova konštanta po známom matematikovi Leonhardovi Eulerovi, ten toto číslo v roku 1727 neobjavil, ale zaviedol mu dodnes známe označenie e a upevnil jeho využitie v teórii logaritmov. Ako prví číslo „našiel“ John Napier, ktorý už v roku 1618 naráža pri výpočtoch logaritmov na túto hodnotu. Eulerova konštanta je podobne ako π iracionálnym a transcendentým číslom. Jej rozvoj je teda nekonečný a nie je riešením žiadnej algebraickej rovnice.
Eulerova rovnosť
S číslami o ktorých sme si dnes niečo málo povedali súvisí aj jeden z najzaujímavejších vzorcov matematiky. Je ním Eulerova rovnosť. V tomto vzorci sa okrem e a π vyskytuje aj ďalší symbol matematiky a to i. i je imaginárna jednotka, ktorá rozširuje obor reálnych čísel na čísla komplexné, s ktorými ste sa možno na stredných školách už nestretli.

Eulerova rovnosť je snáď najzaujímavejší vzorec matematiky a to preto, že sa v ňom objavujú tri základné matematické operácie (sčitovanie, násobenie, mocnina) a všetky najdôležitejšie čísla matematiky (0,1, i, e, π). V tomto vzorci sa každá operácia, aj každé číslo vyskytuje presne jediný krát. Tento vzorec je označovaný aj ako matematický dôkaz existencie Boha…
Ešte stále sa vám zdá matematika nezaujímavá?
Pozri aj: 10 zaujímavostí zo života Alberta Einsteina, ktoré vás presvedčia, že bol poriadny čudák
interez.sk (Lukáš M.)
 23-ročné dievča nakrútilo video, kde sa mračí do kamery, má 46 miliónov lajkov: Môže prekonať rekord Belly Poarch
23-ročné dievča nakrútilo video, kde sa mračí do kamery, má 46 miliónov lajkov: Môže prekonať rekord Belly Poarch Pravidlo 45-25-10-10-10 ti ušetrí peniaze: Takto ľahko si rozdelíš svoj príjem a výdavky a staneš sa finančne nezávislým
Pravidlo 45-25-10-10-10 ti ušetrí peniaze: Takto ľahko si rozdelíš svoj príjem a výdavky a staneš sa finančne nezávislým Kedysi praskal vo švíkoch, natáčali tu aj Fontánu pre Zuzanu: Ikonický motorest dnes chátra, jeho osud spečatila diaľnica
Kedysi praskal vo švíkoch, natáčali tu aj Fontánu pre Zuzanu: Ikonický motorest dnes chátra, jeho osud spečatila diaľnica S detskými herečkami sa kúpal vo vírivke, mal fetiš na ich nohy. Dan Schneider tvoril detské hviezdy, no aj ich zničil
S detskými herečkami sa kúpal vo vírivke, mal fetiš na ich nohy. Dan Schneider tvoril detské hviezdy, no aj ich zničil Za večer poslali ľudia aj milión smsiek. Prvá Superstar spôsobila na Slovensku hystériu, televíziu stála šialenú sumu
Za večer poslali ľudia aj milión smsiek. Prvá Superstar spôsobila na Slovensku hystériu, televíziu stála šialenú sumu Ak by radista išiel spať o 5 minút neskôr, katastrofe mohli predísť. Takto prebiehali posledné hodiny Titanicu
Ak by radista išiel spať o 5 minút neskôr, katastrofe mohli predísť. Takto prebiehali posledné hodiny Titanicu Bára žije v Egypte: Byt sa tu dá kúpiť za 40-tisíc eur, ľudia ale zarábajú aj 40 eur mesačne. Muži môžu mať štyri manželky
Bára žije v Egypte: Byt sa tu dá kúpiť za 40-tisíc eur, ľudia ale zarábajú aj 40 eur mesačne. Muži môžu mať štyri manželky Tvrdil, že vie ženám privodiť najintenzívnejší orgazmus: Zo slávneho hypnotizéra sa vykľul predátor kradnúci nahé fotky
Tvrdil, že vie ženám privodiť najintenzívnejší orgazmus: Zo slávneho hypnotizéra sa vykľul predátor kradnúci nahé fotky Stúpil jej na chrbát a takmer jej nožom odrezal hlavu od tela. O. J. Simpson však vyšiel z procesu storočia ako nevinný
Stúpil jej na chrbát a takmer jej nožom odrezal hlavu od tela. O. J. Simpson však vyšiel z procesu storočia ako nevinný Boli sme v kontroverznej reštaurácii Pekidors z Na nože: Nálepku nedostala, počas obeda bola prázdna. Toto nás prekvapilo
Boli sme v kontroverznej reštaurácii Pekidors z Na nože: Nálepku nedostala, počas obeda bola prázdna. Toto nás prekvapilo






















Nahlásiť chybu v článku